MATEMÁTICAS DISCRETAS

miércoles, 2 de diciembre de 2015

ARBOLES BINARIOS

En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo puede tener un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman.

Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho

ARBOLES DE EXPANSIÓN MÍNIMA

Dado un grafo conexo y no dirigido, un árbol recubridor mínimo de ese grafo es un subgrafo que tiene que ser un árbol y contener todos los vértices del grafo inicial. Cada arista tiene asignado un peso proporcional entre ellos, que es un número representativo de algún objeto, distancia, etc.; y se usa para asignar un peso total al árbol recubridor mínimo computando la suma de todos los pesos de las aristas del árbol en cuestión. Un árbol recubridor mínimo o un árbol expandido mínimo es un árbol recubridor que pesa menos o igual que otros árboles recubridores. Todo grafo tiene un bosque recubridor mínimo.

Un ejemplo sería una compañía de cable trazando cable a una nueva vecindad. Si está limitada a trazar el cable por ciertos caminos, entonces se hará un grafo que represente los puntos conectados por esos caminos. Algunos de estos caminos podrán ser más caros que otros, por ser más largos. Estos caminos serían representados por las aristas con mayores pesos. Un árbol recubridor para este grafo sería un subconjunto de estos caminos que no tenga ciclos pero que mantenga conectadas todas las casas. Puede haber más de un árbol recubridor posible. El árbol recubridor mínimo será el de menos coste.

En el caso de un empate, porque podría haber más de un árbol recubridor mínimo; en particular, si todos los pesos son iguales, todo árbol recubridor será mínimo. De todas formas, si cada arista tiene un peso distinto existirá sólo un árbol recubridor mínimo. La demostración de esto es trivial y se puede hacer porinducción. Esto ocurre en muchas situaciones de la realidad, como con la compañía de cable en el ejemplo anterior, donde es extraño que dos caminos tengan exactamente el mismo coste. Esto también se generaliza para los bosques recubridores.

Si los pesos son positivos, el árbol recubridor mínimo es el subgrafo de menor costo posible conectando todos los vértices, ya que los subgrafos que contienen ciclos necesariamente tienen más peso total.

ARBOLES DE EXPANSION

En teoría de grafos, un árbol de expansión, árbol generador o árbol recubridor T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas) de las aristas de G. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que cubre todos los vértices. Esto es, cada vértice está en el árbol, pero no hay ciclos. Por otro lado, todos los puentes de G deben estar contenidos en T.

Un árbol de expansión o árbol recubridor de un grafo conexo G puede ser también definido como el mayor conjunto de aristas de G que no contiene ciclos, o como el mínimo conjunto de aristas que conecta todos los vértices.

En ciertos campos de la teoría de grafos es útil encontrar el mínimo árbol de expansión de un grafo ponderado. También se han abordado otros problemas de optimización relacionados con los árboles de expansión, como el máximo árbol de expansión, el máximo árbol que cubre al menos k vértices, el mínimo árbol de expansión con k aristas por vértice como máximo (árbol de expansión de mínimo grado, MDST por sus siglas en inglés), el árbol de expansión con el máximo número de hojas (estrechamente relacionado con el problema del menos conjunto dominante y conexo), el árbol de expansión con el menor número de hojas (relacionado con el problema del camino hamiltoniano), el árbol de expansión de mínimo diámetro o el árbol de expansión de la mínima dilación.

ARBOLES

Arboles:

Un árbol es un grafo simple en el cual existe un único camino entre cada par de vértices.

Sea G =(V,A) un grafo no dirigido. G se denomina ARBOL, si es conexo y no contiene ciclos.

Un árbol con raíz, es un árbol que tiene un vértice particular designado como raíz.

Ejemplo de árbol:

En la figura anterior G1 corresponde a lo que llamamos mediante la definición ARBOL, en el caso de G2, éste no corresponde debido a que contiene un ciclo.

Podemos destacar que cuando un grafo G es un Arbol, se reemplaza G, por R.

En la figura mostrada G1 es un subgrafo de G2, en el que G1 contiene los vértices de G2 y es árbol, además lo llamaremos “árbol abarcador”, por que proporciona conexión minimal para el grafo y un esqueleto minimal que une los vértices.

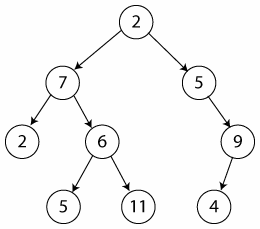
Ejemplo de árbol raíz:

Para apoyar el entendimiento de las definiciones entregadas agregaremos algunos teoremas.

Si a, b son vértices de un árbol R (V,A), entonces hay un camino único que conecta estos vértices.

En cualquier árbol R= (V,A), |V| = |A| + 1.

Para cualquier árbol R = (V,A), si |A| >= 2, entonces R tiene al menos dos vértices colgantes.

Sea G un grafo simple con v vértices, entonces se puede decir:

G es un árbol.
G es conexo y no contiene circuitos.
G es conexo y tiene (n-1) lados.
G no contiene circuitos y tiene (n-1) lados.

Arboles con Raíz

Sea G un grafo dirigido, se denomina “árbol dirigido” si el grafo no dirigido asociado con G es un árbol. Cuando G es un árbol dirigido, se denomina “árbol con raíz” si hay un único vértice r, la raíz.

Sea G un grafo con raíz V0. Supóngase que x, y, z son vértices en G y que (v0, v1, ..., vn), es un camino en G.

V(n-1) es el padre de v(n).
V0, v1, ..., v(n-1) son los antepasados de v(n).
V(n) es el hijo de v(n-1).
Si x es un antepasado de y, entonces y es un descendiente de x.
Si x e y son hijos de z entonces x e y son hermanos.
Si x no tiene hijos entonces x es un vértice terminal.
Si x no es un vértice terminal, entonces x es un vértice interno.
El subgrafo de G que consiste en x y todos sus descendientes, con x como raíz, es el subarbol de G que tiene a x como raíz.

Sea R= (V,A) un árbol con raíz r. Si R no tiene otros vértices, entonces la raíz misma constituye el recorrido en orden previo, simétrico y posterior de R. Si |V| > 1, sean R1, R2, R3, ...., Rk los subarboles de R según se va de izquierda a derecha.

El recorrido de orden previo de R comienza en r y después pasa por los vértices de R1 en orden previo, a continuación por los vértices de R2 en orden previo, y así sucesivamente hasta que se pasa por los vértices de Rk en orden previo.

El recorrido en orden simétrico de R primero, se pasa por los vértices de R1 en orden simétrico, después por la raíz r y a continuación por los vértices de los subarboles R2, R3,...., Rk en orden simétrico.

El recorrido en orden posterior de R pasa por los vértices de los subarboles R1, R2,...., Rk en orden posterior y a continuación por la raíz.

Un árbol binario es uno con raíz en el cual cada vértice tiene un hijo a la derecha o un hijo a la izquierda, o viceversa, o bien ningún hijo. Un árbol binario completo es uno en el cual cada vértice tiene un hijo a la derecha y uno a la izquierda, o bien ningún hijo.

Si T es un árbol binario completo con i vértices internos, entonces T tiene i + 1 vértices terminales y 2i + 1 vértices en total.

Un árbol binario de búsqueda es un árbol binario T donde se han asociado datos a los vértices. Los datos se disponen de manera que para cualquier vértice v en T, cada dato en el subarbol a la izquierda de v es menor que el dato correspondiente a v.

ISOMORFISMO DE GRAFOS

En teoría de grafos, un isomorfismo entre dos grafos G y H es una biyección f entre los conjuntos de sus vértices

f: V(G) \rightarrow V(H)

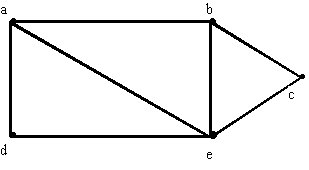
que preserva la relación de adyacencia. Es decir, cualquier par de vérticesu y v de G son adyacentes si y solo si lo son sus imágenes, f(u) y f(v), en H.

A pesar de su diferente aspecto, los dos grafos que se muestran a continuación son isomorfos:

Grafo G	Grafo H	Un isomorfismo entre G y H
		$f(a) = 1$ $f(b) = 6$ $f(c) = 8$ $f(d) = 3$ $f(g) = 5$ $f(h) = 2$ $f(i) = 4$ $f(j) = 7$

Dos grafos con matrices de adyacencia respectivas A y B serán isomofos si y solo si existe una matriz permutación P tal que B = P A P

La determinación de si dos grafos con el mismo número de vértices n y aristas m son isomorfos o no, se conoce como el problema del isomorfismo de grafos. Este problema admite un ataque por fuerza bruta que exigiría comprobar si las n! biyecciones posibles preservan la adyacencia, pero no se conoce un algoritmo eficiente, al menos para el caso general. En este contexto, eficiencia debe interpretarse como crecimiento del número de pasos inferior a O(eⁿ).

El problema del isomorfismo de grafos presenta una curiosidad en teoría de complejidad computacional al ser uno de los pocos problemas citados por Garey y Johnson en 1979 pertenecientes a NP de los que se desconoce si es resoluble en tiempo polinómico o si es NP-completo (actualmente está en revisión la demostración de que el problema está en P)

GRAFOS APLANABLES

Este tipo de grafos, además de aparecer con mucha frecuencia también cuentan con muchas propiedades interesante. Se analizarán algunas de las más importantes.

Diremos que un grafo es aplanable si puede ser dibujado sobre un plano de tal manera tal que ninguna arista se cruce con otra excepto, desde luego, en los vértices comunes. El siguiente es un grafo aplanable:

El grafo también es aplanable ya que puede dibujarse como se muestra en el grafo

CAMINOS Y CICLOS

En Teoría de grafos, un Grafo ciclo o simplemente ciclo es un grafo que se asemeja a un polígono de n lados. Consiste en un camino cerrado en el que no se repite ningún vértice a excepción del primero que aparece dos veces como principio y fin del camino. Un Grafo ciclo de n vértices se denota C_n. El número de vértices en un grafo C_n es igual al número de aristas, y cada vértice tiene grado par, por lo tanto cada vértice tiene dos aristas incidentes.

G(V,A)\,

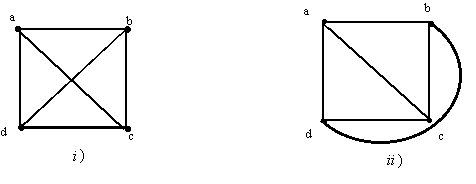
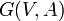es un ciclo C_n, el grafo tiene n vértices

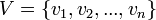V= \{v_1 , v_2 , ... , v_n \} \,

y n aristas formadas de la siguiente manera:

A=\{\{v_i , v_{i+1}\}|i= 1, ..., n\} \cup \{v_n , v_1\}

Un camino es una sucesión de vértices tal que de cada uno de sus vértices existe una arista hacia el vértice sucesor. Un camino simple es aquel que no repite vértices en su recorrido. Dos caminos son ajenos o independientes si no tienen ningún vértice en común excepto el primero y el último. La longitud de un camino es el número de aristas que usa dicho camino, contando aristas recorridas varias veces el mismo número de veces que las recorramos. En el ejemplo, (1, 2, 5, 1, 2, 3) es un camino con longitud 5, y (5, 2, 1) es un camino simple de longitud 2..
Un caminoeuleriano recorre todas las aristas exactamente una vez (puede repetir vértices).	Camino euleriano Un camino euleriano en un grafo es un camino que usa cada arista una y sólo una vez. Si existe tal camino decimos que el grafo es euleriano. Esta definición es dual a la de camino hamiltoniano.
Un camino hamiltonianorecorre todos los vértices exactamente una vez.	Camino hamiltoniano Existe un concepto dual al de camino/ciclo Euleriano. Un camino hamiltoniano en un grafo es un camino que "visita" cada vértice una y sólo una vez.
Orden en que se recorre un grafo en una búsqueda en profundidad.	Ciclo Un Ciclo (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 se denominan lazos o bucles. Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el vértice inicial coincide con el vértice final.
Un ciclo euleriano pasa por todas las aristas exactamente una vez, regresando al punto de partida.	Ciclo euleriano Un ciclo euleriano en un grafo es un ciclo que usa cada arista una y sólo una vez.
Un ciclo hamiltoniano pasa por todos los vértices exactamente una vez, regresando al punto de partida.	Ciclo hamiltoniano Un ciclo hamiltoniano en un grafo es un cic