Se tiene un conjunto con 6 objetos diferentes {A,B,C,D,E,F}, de los cuales se desea escoger 2 (sin importar el orden de elección). Existen 15 formas de efectuar tal elección
| A,B | A,C | A,D | A,E | A,F |
| B,C | B,D | B,E | B,F | |
| C,D | C,E | C,F | ||
| D,E | D,F | |||
| E,F |
El número de formas de escoger k elementos a partir de un conjunto de n, puede denotarse de varias formas:nota 2  ,
,  ,
, 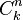 , o
, o  . Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de escoger 2 objetos a partir de un conjunto con 6 elementos.
. Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de escoger 2 objetos a partir de un conjunto con 6 elementos.
 ,
,  ,
, 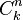 , o
, o  . Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de escoger 2 objetos a partir de un conjunto con 6 elementos.
. Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de escoger 2 objetos a partir de un conjunto con 6 elementos.
Los números C(n,k) se conocen como «coeficientes binomiales», pero es frecuente referirse a ellos como «combinaciones de n en k», o simplemente «n en k». Por tanto, la primera definición es:
El coeficiente binomial  es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
 es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
el teorema del binomio es una fórmula que proporciona el desarrollo de la potencia n-ésima de n (siendo n, entero positivo) de un binomio. De acuerdo con el teorema, es posible expandir lapotencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son números naturales con b + c = n, y el coeficiente a de cada término es un número entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
El coeficiente a en los términos de xbyc - xcyb es conocido como el coeficiente binomial 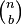 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
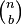 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
No hay comentarios:
Publicar un comentario