En
Teoría de grafos, un
Grafo ciclo o simplemente
ciclo es un
grafo que se asemeja a un polígono de
n lados. Consiste en un camino cerrado en el que no se repite ningún vértice a excepción del primero que aparece dos veces como principio y fin del camino. Un Grafo ciclo de
n vértices se denota
Cn. El número de vértices en un grafo C
n es igual al número de aristas, y cada vértice tiene grado par, por lo tanto cada vértice tiene dos aristas incidentes.
si
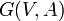
es un ciclo C
n, el grafo tiene
n vértices
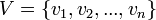
y
n aristas formadas de la siguiente manera:

- Un camino es una sucesión de vértices tal que de cada uno de sus vértices existe una arista hacia el vértice sucesor. Un camino simple es aquel que no repite vértices en su recorrido.
- Dos caminos son ajenos o independientes si no tienen ningún vértice en común excepto el primero y el último.
- La longitud de un camino es el número de aristas que usa dicho camino, contando aristas recorridas varias veces el mismo número de veces que las recorramos. En el ejemplo, (1, 2, 5, 1, 2, 3) es un camino con longitud 5, y (5, 2, 1) es un camino simple de longitud 2..
|

Un caminoeuleriano recorre todas las aristas exactamente una vez (puede repetir vértices).
|
Camino euleriano
- Un camino euleriano en un grafo es un camino que usa cada arista una y sólo una vez. Si existe tal camino decimos que el grafo es euleriano. Esta definición es dual a la de camino hamiltoniano.
|

Un camino hamiltonianorecorre todos los vértices exactamente una vez.
|
Camino hamiltoniano
- Existe un concepto dual al de camino/ciclo Euleriano. Un camino hamiltoniano en un grafo es un camino que "visita" cada vértice una y sólo una vez.
|

Orden en que se recorre un grafo en una búsqueda en profundidad.
|
Ciclo
- Un Ciclo (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 se denominan lazos o bucles.
- Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el vértice inicial coincide con el vértice final.
|

Un ciclo euleriano pasa por todas las aristas exactamente una vez, regresando al punto de partida.
|
Ciclo euleriano
- Un ciclo euleriano en un grafo es un ciclo que usa cada arista una y sólo una vez.
|

Un ciclo hamiltoniano pasa por todos los vértices exactamente una vez, regresando al punto de partida.
|
Ciclo hamiltoniano
- Un ciclo hamiltoniano en un grafo es un cic
|
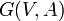 es un ciclo Cn, el grafo tiene n vértices
es un ciclo Cn, el grafo tiene n vértices 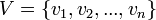 y n aristas formadas de la siguiente manera:
y n aristas formadas de la siguiente manera: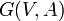 es un ciclo Cn, el grafo tiene n vértices
es un ciclo Cn, el grafo tiene n vértices 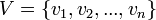 y n aristas formadas de la siguiente manera:
y n aristas formadas de la siguiente manera:





No hay comentarios:
Publicar un comentario